What is the VSEPR theory used to predict?

Example of bent electron arrangement. Shows location of unpaired electrons, bonded atoms, and bond angles. (Water molecule) The bond bending for water is 104.v°.
Valence shell electron pair repulsion (VSEPR) theory ( VESP-ər,[1] : 410 və-SEP-ər [2]), is a model used in chemistry to predict the geometry of individual molecules from the number of electron pairs surrounding their central atoms.[3] It is too named the Gillespie-Nyholm theory after its ii main developers, Ronald Gillespie and Ronald Nyholm.
The premise of VSEPR is that the valence electron pairs surrounding an atom tend to repel each other and will, therefore, adopt an arrangement that minimizes this repulsion. This in turn decreases the molecule's energy and increases its stability, which determines the molecular geometry. Gillespie has emphasized that the electron-electron repulsion due to the Pauli exclusion principle is more than important in determining molecular geometry than the electrostatic repulsion.[4]
The insights of VSEPR theory are derived from topological assay of the electron density of molecules. Such quantum chemic topology (QCT) methods include the electron localization function (ELF) and the quantum theory of atoms in molecules (AIM or QTAIM).[4] [v] Hence, VSEPR is unrelated to wave office based methods such as orbital hybridisation in valence bond theory.[6]
History [edit]
The idea of a correlation between molecular geometry and number of valence electron pairs (both shared and unshared pairs) was originally proposed in 1939 by Ryutaro Tsuchida in Japan,[7] and was independently presented in a Bakerian Lecture in 1940 by Nevil Sidgwick and Herbert Powell of the University of Oxford.[viii] In 1957, Ronald Gillespie and Ronald Sydney Nyholm of University Higher London refined this concept into a more than detailed theory, capable of choosing between various alternative geometries.[9] [ten]
Overview [edit]
VSEPR theory is used to predict the system of electron pairs around central atoms in molecules, especially simple and symmetric molecules. A cardinal atom is divers in this theory every bit an atom which is bonded to two or more than other atoms, while a terminal atom is bonded to only one other atom.[i] : 398 For instance in the molecule methyl isocyanate (H3C-N=C=O), the ii carbons and 1 nitrogen are central atoms, and the three hydrogens and one oxygen are terminal atoms.[one] : 416 The geometry of the primal atoms and their non-bonding electron pairs in plough make up one's mind the geometry of the larger whole molecule.
The number of electron pairs in the valence shell of a central atom is determined subsequently drawing the Lewis construction of the molecule, and expanding information technology to show all bonding groups and lone pairs of electrons.[1] : 410–417 In VSEPR theory, a double bond or triple bond is treated as a unmarried bonding group.[1] The sum of the number of atoms bonded to a central atom and the number of lone pairs formed by its nonbonding valence electrons is known as the central atom'due south steric number.
The electron pairs (or groups if multiple bonds are nowadays) are assumed to prevarication on the surface of a sphere centered on the central atom and tend to occupy positions that minimize their common repulsions by maximizing the distance between them.[1] : 410–417 [11] The number of electron pairs (or groups), therefore, determines the overall geometry that they will adopt. For example, when there are two electron pairs surrounding the primal cantlet, their mutual repulsion is minimal when they lie at opposite poles of the sphere. Therefore, the central cantlet is predicted to adopt a linear geometry. If at that place are 3 electron pairs surrounding the central atom, their repulsion is minimized by placing them at the vertices of an equilateral triangle centered on the atom. Therefore, the predicted geometry is trigonal. Besides, for 4 electron pairs, the optimal arrangement is tetrahedral.[1] : 410–417
Equally a tool in predicting the geometry adopted with a given number of electron pairs, an oft used physical demonstration of the principle of minimal electron pair repulsion utilizes inflated balloons. Through handling, balloons acquire a slight surface electrostatic accuse that results in the adoption of roughly the same geometries when they are tied together at their stems as the respective number of electron pairs. For case, v balloons tied together adopt the trigonal bipyramidal geometry, merely as do the five bonding pairs of a PCl5 molecule.
Steric number [edit]
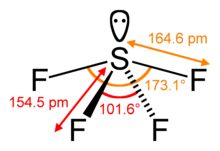
Sulfur tetrafluoride has a steric number of 5.
The steric number of a primal atom in a molecule is the number of atoms bonded to that central atom, called its coordination number, plus the number of solitary pairs of valence electrons on the central atom.[12] In the molecule SF4, for example, the central sulfur atom has four ligands; the coordination number of sulfur is iv. In addition to the four ligands, sulfur also has one lonely pair in this molecule. Thus, the steric number is iv + 1 = 5.
Degree of repulsion [edit]
The overall geometry is farther refined by distinguishing between bonding and nonbonding electron pairs. The bonding electron pair shared in a sigma bail with an adjacent atom lies further from the central atom than a nonbonding (solitary) pair of that atom, which is held close to its positively charged nucleus. VSEPR theory therefore views repulsion past the lone pair to be greater than the repulsion by a bonding pair. Every bit such, when a molecule has 2 interactions with different degrees of repulsion, VSEPR theory predicts the construction where lone pairs occupy positions that let them to experience less repulsion. Solitary pair–alone pair (lp–lp) repulsions are considered stronger than lonely pair–bonding pair (lp–bp) repulsions, which in plough are considered stronger than bonding pair–bonding pair (bp–bp) repulsions, distinctions that and so guide decisions about overall geometry when 2 or more than non-equivalent positions are possible.[i] : 410–417 For instance, when 5 valence electron pairs environment a key atom, they adopt a trigonal bipyramidal molecular geometry with two collinear axial positions and three equatorial positions. An electron pair in an centric position has three close equatorial neighbors just 90° away and a fourth much further at 180°, while an equatorial electron pair has only two adjacent pairs at 90° and two at 120°. The repulsion from the close neighbors at ninety° is more than important, so that the axial positions feel more repulsion than the equatorial positions; hence, when there are lone pairs, they tend to occupy equatorial positions as shown in the diagrams of the next department for steric number 5.[11]
The difference betwixt lone pairs and bonding pairs may also be used to rationalize deviations from idealized geometries. For example, the H2O molecule has four electron pairs in its valence shell: two lone pairs and ii bail pairs. The four electron pairs are spread so as to signal roughly towards the apices of a tetrahedron. However, the bail bending between the ii O–H bonds is only 104.5°, rather than the 109.5° of a regular tetrahedron, considering the 2 lone pairs (whose density or probability envelopes lie closer to the oxygen nucleus) exert a greater mutual repulsion than the ii bond pairs.[one] : 410–417 [11]
A bail of higher bond club besides exerts greater repulsion since the pi bond electrons contribute.[xi] For example in isobutylene, (HiiiC)2C=CH2, the H3C−C=C angle (124°) is larger than the H3C−C−CHiii bending (111.5°). However, in the carbonate ion, CO 2−
3 , all iii C−O bonds are equivalent with angles of 120° due to resonance.
AXE method [edit]
The "AXE method" of electron counting is commonly used when applying the VSEPR theory. The electron pairs effectually a cardinal atom are represented by a formula AXdue northEm, where A represents the key atom and e'er has an implied subscript one. Each X represents a ligand (an atom bonded to A). Each E represents a lonely pair of electrons on the central cantlet.[ane] : 410–417 The total number of X and E is known as the steric number. For example in a molecule AXthreeE2, the cantlet A has a steric number of v.
When the substituent (Ten) atoms are not all the same, the geometry is still approximately valid, merely the bond angles may exist slightly dissimilar from the ones where all the outside atoms are the same. For example, the double-bond carbons in alkenes like C2H4 are AXiiiE0, but the bond angles are not all exactly 120°. Likewise, SOCl2 is AX3Ei, but considering the X substituents are not identical, the 10–A–X angles are not all equal.
Based on the steric number and distribution of Tens and Eastwards, VSEPR theory makes the predictions in the following tables.
Main-grouping elements [edit]
For principal-group elements, there are stereochemically active lone pairs E whose number tin vary betwixt 0 to three. Note that the geometries are named co-ordinate to the diminutive positions only and not the electron organisation. For example, the description of AX2E1 as a bent molecule means that the three atoms AX2 are not in one straight line, although the lone pair helps to determine the geometry.
| Steric number | Molecular geometry[thirteen] 0 solitary pairs | Molecular geometry[1] : 413–414 one lonely pair | Molecular geometry[1] : 413–414 2 alone pairs | Molecular geometry[1] : 413–414 three lone pairs |
|---|---|---|---|---|
| 2 | | |||
| 3 |  |  | ||
| iv | 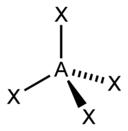 |  |  | |
| 5 |  | 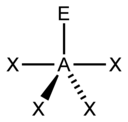 |  |  |
| six | 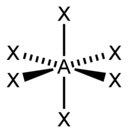 |  |  | |
| vii |  | 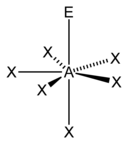 | 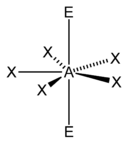 | |
| 8 | | |
| Molecule type | Shape[1] : 413–414 | Electron arrangement[one] : 413–414 including lonely pairs, shown in pale yellow | Geometry[1] : 413–414 excluding lone pairs | Examples |
|---|---|---|---|---|
| AX2Due east0 | Linear | | | BeCl2,[iii] COtwo [xi] |
| AX2E1 | Bent |  |  | NO − 2 ,[3] SO2,[1] : 413–414 O3,[three] CCl2 |
| AX2Eii | Bent | 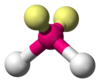 |  | HtwoO,[1] : 413–414 OF2 [14] : 448 |
| AX2E3 | Linear |  | | XeF2,[one] : 413–414 I − 3 ,[14] : 483 XeClii |
| AX3E0 | Trigonal planar |  |  | BF3,[1] : 413–414 CO 2− 3 ,[xiv] : 368 NO − 3 ,[iii] SO3 [11] |
| AX3E1 | Trigonal pyramidal |  |  | NH3,[1] : 413–414 PCl3 [xiv] : 407 |
| AXthreeEast2 | T-shaped |  |  | ClF3,[i] : 413–414 BrF3 [xiv] : 481 |
| AX4E0 | Tetrahedral | 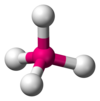 |  | CH4,[one] : 413–414 PO 3− 4 , And then 2− 4 ,[11] ClO − 4 ,[3] XeO4 [xiv] : 499 |
| AXfourE1 | Seesaw or disphenoidal |  | 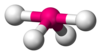 | SFiv [1] : 413–414 [fourteen] : 45 |
| AXfourE2 | Square planar |  |  | XeF4 [1] : 413–414 |
| AXfiveE0 | Trigonal bipyramidal |  |  | PClfive [ane] : 413–414 |
| AX5Eastward1 | Square pyramidal | 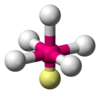 | 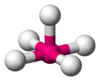 | ClF5,[14] : 481 BrF5,[1] : 413–414 XeOFiv [xi] |
| AX5E2 | Pentagonal planar |  |  | XeF − 5 [fourteen] : 498 |
| AX6E0 | Octahedral | 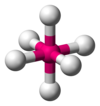 | 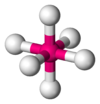 | SFvi [ane] : 413–414 |
| AXhalf-dozenE1 | Pentagonal pyramidal |  |  | XeOF − 5 ,[fifteen] IOF two− 5 [fifteen] |
| AX7E0 | Pentagonal bipyramidal[xi] | 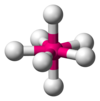 | 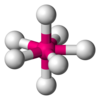 | IFvii [11] |
| AX8E0 | Square antiprismatic[xi] |  |  | IF − 8 , XeFeight 2- in (NO)2XeFeight |
Transition metals (Kepert model) [edit]
The lone pairs on transition element atoms are normally stereochemically inactive, significant that their presence does not change the molecular geometry. For example, the hexaaquo complexes K(HiiO)6 are all octahedral for M = V3+, Mn3+, Co3+, Nitwo+ and Zn2+, despite the fact that the electronic configurations of the central metal ion are d2, div, d6, d8 and d10 respectively.[14] : 542 The Kepert model ignores all lone pairs on transition metal atoms, so that the geometry around all such atoms corresponds to the VSEPR geometry for AXn with 0 lonely pairs E.[16] [fourteen] : 542 This is often written MLn, where Thousand = metal and Fifty = ligand. The Kepert model predicts the following geometries for coordination numbers of ii through 9:
| Molecule blazon | Shape | Geometry | Examples |
|---|---|---|---|
| AXtwo | Linear | | HgCl2 [3] |
| AX3 | Trigonal planar |  | |
| AXiv | Tetrahedral |  | NiCl 2− iv |
| AXfive | Trigonal bipyramidal |  | Fe(CO) 5 |
| Foursquare pyramidal |  | MnClfive 2− | |
| AXsix | Octahedral |  | WCl6 [xiv] : 659 |
| AX7 | Pentagonal bipyramidal[11] |  | ZrF 3− 7 |
| Capped octahedral |  | MoF − 7 | |
| Capped trigonal prismatic | 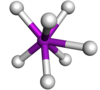 | TaF 2− vii | |
| AX8 | Square antiprismatic[eleven] |  | ReF − 8 |
| Dodecahedral |  | Mo(CN) four− 8 | |
| Bicapped trigonal prismatic | 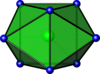 | ZrF 4− 8 | |
| AX9 | Tricapped trigonal prismatic | 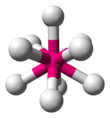 | ReH ii− 9 [xiv] : 254 |
| Capped foursquare antiprismatic |  |
Examples [edit]
The methane molecule (CH4) is tetrahedral considering in that location are 4 pairs of electrons. The iv hydrogen atoms are positioned at the vertices of a tetrahedron, and the bond angle is cos−1(− ane⁄iii ) ≈ 109° 28′.[17] [xviii] This is referred to equally an AXiv type of molecule. As mentioned above, A represents the central atom and Ten represents an outer atom.[1] : 410–417
The ammonia molecule (NH3) has three pairs of electrons involved in bonding, but there is a lone pair of electrons on the nitrogen atom.[one] : 392–393 It is not bonded with some other atom; however, it influences the overall shape through repulsions. Equally in methyl hydride to a higher place, there are 4 regions of electron density. Therefore, the overall orientation of the regions of electron density is tetrahedral. On the other hand, there are only three outer atoms. This is referred to as an AX3E blazon molecule because the lone pair is represented by an E.[1] : 410–417 By definition, the molecular shape or geometry describes the geometric system of the atomic nuclei only, which is trigonal-pyramidal for NHthree.[1] : 410–417
Steric numbers of 7 or greater are possible, but are less common. The steric number of seven occurs in iodine heptafluoride (IF7); the base geometry for a steric number of 7 is pentagonal bipyramidal.[11] The most common geometry for a steric number of 8 is a square antiprismatic geometry.[19] : 1165 Examples of this include the octacyanomolybdate (Mo(CN) four−
8 ) and octafluorozirconate (ZrF iv−
8 ) anions.[nineteen] : 1165 The nonahydridorhenate ion (ReH two−
ix ) in potassium nonahydridorhenate is a rare example of a chemical compound with a steric number of 9, which has a tricapped trigonal prismatic geometry.[14] : 254 [19]
Possible geometries for steric numbers of x, 11, 12, or 14 are bicapped foursquare antiprismatic (or bicapped dodecadeltahedral), octadecahedral, icosahedral, and bicapped hexagonal antiprismatic, respectively. No compounds with steric numbers this loftier involving monodentate ligands exist, and those involving multidentate ligands tin can often be analysed more just as complexes with lower steric numbers when some multidentate ligands are treated every bit a unit.[xix] : 1165, 1721
Exceptions [edit]
There are groups of compounds where VSEPR fails to predict the right geometry.
Some AX2E0 molecules [edit]
The shapes of heavier Group fourteen element alkyne analogues (RM≡MR, where Chiliad = Si, Ge, Sn or Pb) have been computed to exist bent.[twenty] [21] [22]
Some AXiiEii molecules [edit]
Ane instance of the AX2Eii geometry is molecular lithium oxide, Li2O, a linear rather than bent construction, which is ascribed to its bonds being essentially ionic and the stiff lithium-lithium repulsion that results.[23] Another example is O(SiH3)2 with an Si–O–Si bending of 144.1°, which compares to the angles in Cl2O (110.nine°), (CHiii)iiO (111.vii°), and North(CHthree)3 (110.9°).[24] Gillespie and Robinson rationalize the Si–O–Si bond angle based on the observed power of a ligand's lonely pair to most greatly repel other electron pairs when the ligand electronegativity is greater than or equal to that of the key atom.[24] In O(SiH3)2, the cardinal atom is more electronegative, and the lone pairs are less localized and more weakly repulsive. The larger Si–O–Si bond angle results from this and stiff ligand-ligand repulsion by the relatively big -SiHiii ligand.[24] Burford et al showed through X-ray diffraction studies that Cl3Al–O–PCl3 has a linear Al–O–P bond angle and is therefore a non-VSEPR molecule.[ citation needed ]
Some AX6Eastone and AX8Due easti molecules [edit]

Some AX6Eone molecules, e.grand. xenon hexafluoride (XeF6) and the Te(Four) and Bi(III) anions, TeCl 2−
6 , TeBr 2−
six , BiCl 3−
6 , BiBr 3−
vi and BiI three−
half-dozen , are octahedral, rather than pentagonal pyramids, and the lone pair does not affect the geometry to the caste predicted past VSEPR.[25] Similarly, the octafluoroxenate ion (XeF 2−
8 ) in nitrosonium octafluoroxenate(VI)[fourteen] : 498 [26] [27] is a square antiprism and not a bicapped trigonal prism (every bit predicted past VSEPR theory for an AX8East1 molecule), despite having a lone pair. One rationalization is that steric crowding of the ligands allows piddling or no room for the non-bonding lonely pair;[24] another rationalization is the inert pair effect.[14] : 214
Square planar transition metal complexes [edit]
The Kepert model predicts that AX4 transition element molecules are tetrahedral in shape, and it cannot explicate the germination of square planar complexes.[fourteen] : 542 The majority of such complexes exhibit a d8 configuration as for the tetrachloroplatinate (PtCl 2−
4 ) ion. The caption of the shape of foursquare planar complexes involves electronic effects and requires the use of crystal field theory.[14] : 562–iv
Complexes with stiff d-contribution [edit]

Hexamethyltungsten, a transition metal complex whose geometry is different from main-grouping coordination.
Some transition metal complexes with low d electron count accept unusual geometries, which tin be ascribed to d subshell bonding interaction.[28] Gillespie found that this interaction produces bonding pairs that as well occupy the respective antipodal points (ligand opposed) of the sphere.[29] [4] This miracle is an electronic event resulting from the bilobed shape of the underlying sdx hybrid orbitals.[30] [31] The repulsion of these bidirectional bonding pairs leads to a different prepare of shapes.
| Molecule blazon | Shape | Geometry | Examples |
|---|---|---|---|
| AXtwo | Bent |  | VO + ii |
| AXthree | Trigonal pyramidal |  | CrO3 |
| AXfour | Tetrahedral |  | TiCl4 [14] : 598–599 |
| AX5 | Square pyramidal |  | Ta(CH3)5 [32] |
| AXhalf dozen | C3v Trigonal prismatic |  | West(CH3)6 [33] |
The gas phase structures of the triatomic halides of the heavier members of grouping 2, (i.e., calcium, strontium and barium halides, MX2), are non linear as predicted but are bent, (judge Ten–M–X angles: CaF2, 145°; SrF2, 120°; BaFtwo, 108°; SrCl2, 130°; BaCltwo, 115°; BaBrii, 115°; BaI2, 105°).[34] Information technology has been proposed by Gillespie that this is as well caused by bonding interaction of the ligands with the d subshell of the metal cantlet, thus influencing the molecular geometry.[24] [35]
Superheavy elements [edit]
Relativistic effects on the electron orbitals of superheavy elements is predicted to influence the molecular geometry of some compounds. For example, the 6d5/2 electrons in nihonium play an unexpectedly strong role in bonding, so NhFthree should assume a T-shaped geometry, instead of a trigonal planar geometry like its lighter congener BFthree.[36] In contrast, the actress stability of the 7p1/2 electrons in tennessine are predicted to make TsF3 trigonal planar, unlike the T-shaped geometry observed for IFthree and predicted for AtF3;[37] similarly, OgFiv should have a tetrahedral geometry, while XeFiv has a square planar geometry and RnF4 is predicted to take the same.[38]
Odd-electron molecules [edit]
The VSEPR theory tin exist extended to molecules with an odd number of electrons by treating the unpaired electron as a "half electron pair" — for example, Gillespie and Nyholm[9] : 364–365 suggested that the decrease in the bail angle in the series NO +
2 (180°), NO2 (134°), NO −
2 (115°) indicates that a given prepare of bonding electron pairs exert a weaker repulsion on a unmarried non-bonding electron than on a pair of not-bonding electrons. In upshot, they considered nitrogen dioxide equally an AX2E0.5 molecule, with a geometry intermediate between NO +
two and NO −
ii . Similarly, chlorine dioxide (ClO2) is an AXtwoEastwardone.5 molecule, with a geometry intermediate betwixt ClO +
2 and ClO −
2 .[ citation needed ]
Finally, the methyl radical (CH3) is predicted to be trigonal pyramidal similar the methyl anion (CH −
3 ), just with a larger bail angle (as in the trigonal planar methyl cation (CH +
3 )). However, in this instance, the VSEPR prediction is not quite true, as CH3 is actually planar, although its distortion to a pyramidal geometry requires very little free energy.[39]
See as well [edit]
- Valence Bail Theory (VBT)
- Molecular Orbital Theory (MOT)
- Bent's rule (effect of ligand electronegativity)
- Linear combination of atomic orbitals
- Molecular geometry
- Molecular modelling
- Software for molecular modeling
- Thomson trouble
- Valency interaction formula
References [edit]
- ^ a b c d e f g h i j one thousand 50 m n o p q r s t u v west x y z aa ab ac ad ae af Petrucci, R. H.; W. S., Harwood; F. Thousand., Herring (2002). General Chemistry: Principles and Modern Applications (8th ed.). Prentice-Hall. ISBN978-0-13-014329-7.
- ^ Stoker, H. Stephen (2009). Full general, Organic, and Biological Chemistry. Cengage Learning. p. 119. ISBN978-0-547-15281-three.
- ^ a b c d e f m Jolly, W. 50. (1984). Modern Inorganic Chemistry. McGraw-Hill. pp. 77–90. ISBN978-0-07-032760-three.
- ^ a b c Gillespie, R. J. (2008). "50 years of the VSEPR model". Coord. Chem. Rev. 252 (12–14): 1315–1327. doi:10.1016/j.ccr.2007.07.007.
- ^ Bader, Richard F. W.; Gillespie, Ronald J.; MacDougall, Preston J. (1988). "A physical basis for the VSEPR model of molecular geometry". J. Am. Chem. Soc. 110 (22): 7329–7336. doi:x.1021/ja00230a009.
- ^ Gillespie, R. J. (2004), "Teaching molecular geometry with the VSEPR model", J. Chem. Educ., 81 (3): 298–304, Bibcode:2004JChEd..81..298G, doi:x.1021/ed081p298
- ^ Tsuchida, Ryutarō (1939). "A New Simple Theory of Valency" 新簡易原子價論 [New simple valency theory]. Nihon Kagaku Kaishi (in Japanese). 60 (three): 245–256. doi:10.1246/nikkashi1921.60.245.
- ^ Sidgwick, North. V.; Powell, H. Thou. (1940). "Bakerian Lecture. Stereochemical Types and Valency Groups". Proc. Roy. Soc. A. 176 (965): 153–180. Bibcode:1940RSPSA.176..153S. doi:x.1098/rspa.1940.0084.
- ^ a b Gillespie, R. J.; Nyholm, R. Due south. (1957). "Inorganic stereochemistry". Q. Rev. Chem. Soc. 11 (4): 339. doi:10.1039/QR9571100339.
- ^ Gillespie, R. J. (1970). "The electron-pair repulsion model for molecular geometry". J. Chem. Educ. 47 (1): eighteen. Bibcode:1970JChEd..47...18G. doi:x.1021/ed047p18.
- ^ a b c d e f g h i j g l m n Miessler, G. 50.; Tarr, D. A. (1999). Inorganic Chemistry (2nd ed.). Prentice-Hall. pp. 54–62. ISBN978-0-13-841891-5.
- ^ Miessler, 1000. Fifty.; Tarr, D. A. (1999). Inorganic Chemistry (2nd ed.). Prentice-Hall. p. 55. ISBN978-0-xiii-841891-5.
- ^ Petrucci, R. H.; W. South., Harwood; F. Thousand., Herring (2002). Full general Chemical science: Principles and Modern Applications (8th ed.). Prentice-Hall. pp. 413–414 (Tabular array 11.one). ISBN978-0-xiii-014329-7.
- ^ a b c d e f m h i j k l m northward o p q r s Housecroft, C. Eastward.; Sharpe, A. K. (2005). Inorganic Chemistry (2nd ed.). Pearson. ISBN978-0-130-39913-7.
- ^ a b Baran, E. (2000). "Mean amplitudes of vibration of the pentagonal pyramidal XeOF −
5 and IOF two−
five anions". J. Fluorine Chem. 101: 61–63. doi:10.1016/S0022-1139(99)00194-iii. - ^ Anderson, O. P. (1983). "Book reviews: Inorganic Stereochemistry (by David 50. Kepert)" (PDF). Acta Crystallographica B. 39: 527–528. doi:10.1107/S0108768183002864 . Retrieved fourteen September 2020.
based on a systematic quantitative application of the mutual ideas regarding electron-pair repulsion
- ^ Brittin, W. E. (1945). "Valence Angle of the Tetrahedral Carbon Atom". J. Chem. Educ. 22 (3): 145. Bibcode:1945JChEd..22..145B. doi:ten.1021/ed022p145.
- ^ "Bending Between 2 Legs of a Tetrahedron" Archived 2018-10-03 at the Wayback Machine – Maze5.net
- ^ a b c d Wiberg, E.; Holleman, A. F. (2001). Inorganic Chemistry. Bookish Press. ISBN978-0-12-352651-ix.
- ^ Power, Philip P. (September 2003). "Silicon, germanium, tin and lead analogues of acetylenes". Chem. Commun. (17): 2091–2101. doi:10.1039/B212224C. PMID 13678155.
- ^ Nagase, Shigeru; Kobayashi, Kaoru; Takagi, Nozomi (6 October 2000). "Triple bonds between heavier Grouping 14 elements. A theoretical arroyo". J. Organomet. Chem. 11 (1–2): 264–271. doi:ten.1016/S0022-328X(00)00489-7.
- ^ Sekiguchi, Akira; Kinjō, Rei; Ichinohe, Masaaki (September 2004). "A Stable Compound Containing a Silicon–Silicon Triple Bail" (PDF). Science. 305 (5691): 1755–1757. Bibcode:2004Sci...305.1755S. doi:10.1126/scientific discipline.1102209. PMID 15375262. S2CID 24416825. [ permanent dead link ]
- ^ Bellert, D.; Breckenridge, W. H. (2001). "A spectroscopic determination of the bail length of the LiOLi molecule: Strong ionic bonding". J. Chem. Phys. 114 (7): 2871. Bibcode:2001JChPh.114.2871B. doi:10.1063/i.1349424.
- ^ a b c d e Gillespie, R. J.; Robinson, E. A. (2005). "Models of molecular geometry". Chem. Soc. Rev. 34 (5): 396–407. doi:ten.1039/b405359c. PMID 15852152.
- ^ Wells, A. F. (1984). Structural Inorganic Chemistry (5th ed.). Oxford Scientific discipline Publications. ISBN978-0-19-855370-0.
- ^ Peterson, W.; Holloway, H.; Coyle, A.; Williams, G. (Sep 1971). "Antiprismatic Coordination almost Xenon: the Structure of Nitrosonium Octafluoroxenate(VI)". Science. 173 (4003): 1238–1239. Bibcode:1971Sci...173.1238P. doi:10.1126/scientific discipline.173.4003.1238. ISSN 0036-8075. PMID 17775218. S2CID 22384146.
- ^ Hanson, Robert K. (1995). Molecular origami: precision scale models from paper. University Science Books. ISBN978-0-935702-xxx-9.
- ^ Kaupp, Martin (2001). ""Non-VSEPR" Structures and Bonding in d0 Systems". Angew. Chem. Int. Ed. Engl. 40 (1): 3534–3565. doi:10.1002/1521-3773(20011001)twoscore:19<3534::Assistance-ANIE3534>3.0.CO;2-#.
- ^ Gillespie, Ronald J.; Noury, Stéphane; Pilmé, Julien; Silvi, Bernard (2004). "An Electron Localization Function Study of the Geometry of d0 Molecules of the Catamenia 4 Metals Ca to Mn". Inorg. Chem. 43 (10): 3248–3256. doi:10.1021/ic0354015. PMID 15132634.
- ^ Landis, C. R.; Cleveland, T.; Firman, T. Thou. (1995). "Making sense of the shapes of simple metal hydrides". J. Am. Chem. Soc. 117 (6): 1859–1860. doi:x.1021/ja00111a036.
- ^ Landis, C. R.; Cleveland, T.; Firman, T. K. (1996). "Structure of W(CH3)6". Science. 272 (5259): 179–183. doi:10.1126/science.272.5259.179f.
- ^ Rex, R. Bruce (2000). "Diminutive orbitals, symmetry, and coordination polyhedra". Coord. Chem. Rev. 197: 141–168. doi:10.1016/s0010-8545(99)00226-x.
- ^ Haalan, A.; Hammel, A.; Rydpal, Grand.; Volden, H. V. (1990). "The coordination geometry of gaseous hexamethyltungsten is non octahedral". J. Am. Chem. Soc. 112 (11): 4547–4549. doi:ten.1021/ja00167a065.
- ^ Greenwood, Norman Northward.; Earnshaw, Alan (1997). Chemical science of the Elements (2nd ed.). Butterworth-Heinemann. ISBN978-0-08-037941-viii.
- ^ Seijo, Luis; Barandiarán, Zoila; Huzinaga, Sigeru (1991). "Ab initio model potential written report of the equilibrium geometry of alkaline metal earth dihalides: MX2 (1000=Mg, Ca, Sr, Ba; 10=F, Cl, Br, I)" (PDF). J. Chem. Phys. 94 (5): 3762. Bibcode:1991JChPh..94.3762S. doi:x.1063/1.459748. hdl:10486/7315.
- ^ Seth, Michael; Schwerdtfeger, Peter; Fægri, Knut (1999). "The chemical science of superheavy elements. III. Theoretical studies on element 113 compounds". Journal of Chemical Physics. 111 (fourteen): 6422–6433. Bibcode:1999JChPh.111.6422S. doi:10.1063/1.480168. S2CID 41854842.
- ^ Bae, Ch.; Han, Y.-1000.; Lee, Yo. S. (18 January 2003). "Spin−Orbit and Relativistic Effects on Structures and Stabilities of Group 17 Fluorides EF3 (Due east = I, At, and Element 117): Relativity Induced Stability for the D3h Structure of (117)F3". The Journal of Physical Chemistry A. 107 (6): 852–858. Bibcode:2003JPCA..107..852B. doi:10.1021/jp026531m.
- ^ Han, Immature-Kyu; Lee, Yoon Sup (1999). "Structures of RgFn (Rg = Xe, Rn, and Chemical element 118. n = ii, 4.) Calculated by Two-component Spin-Orbit Methods. A Spin-Orbit Induced Isomer of (118)Ffour". Periodical of Concrete Chemistry A. 103 (eight): 1104–1108. Bibcode:1999JPCA..103.1104H. doi:10.1021/jp983665k.
- ^ Anslyn, Due east. V.; Dougherty, D. A. (2006). Modernistic Physical Organic Chemistry. University Science Books. p. 57. ISBN978-1891389313.
Further reading [edit]
- Lagowski, J. J., ed. (2004). Chemistry: Foundations and Applications . Vol. 3. New York: Macmillan. pp. 99–104. ISBN978-0-02-865721-nine.
External links [edit]
- VSEPR AR - 3D VSEPR Theory Visualization with Augmented Reality app
- 3D Chem – Chemistry, structures, and 3D Molecules
- IUMSC – Indiana University Molecular Structure Heart
Source: https://en.wikipedia.org/wiki/VSEPR_theory
Postar um comentário for "What is the VSEPR theory used to predict?"